5.06 Solve rational equations
Solve rational equations
A rational equation is any equation containing at least one rational expression.
When working algebraically to find solutions we can get viable, non-viable, and/or extraneous solutions.
For rational equations, extraneous solutions typically occur at values which make both the numerator and denominator of a rational expression equal to 0. That is, for f\left(x\right)=\dfrac{P\left(x\right)}{Q\left(x\right)}, if we have that {P\left(a\right)=0} and Q\left(a\right)=0, then x=a is extraneous.
We can identify extraneous solutions by substituting all solutions back into the original equation. If a value does not make the equation true, then it is extraneous.
When solving rational equations, it is important to keep in mind both the algebraic restrictions on the variables as well as any context involved in the question.
Examples
Example 1
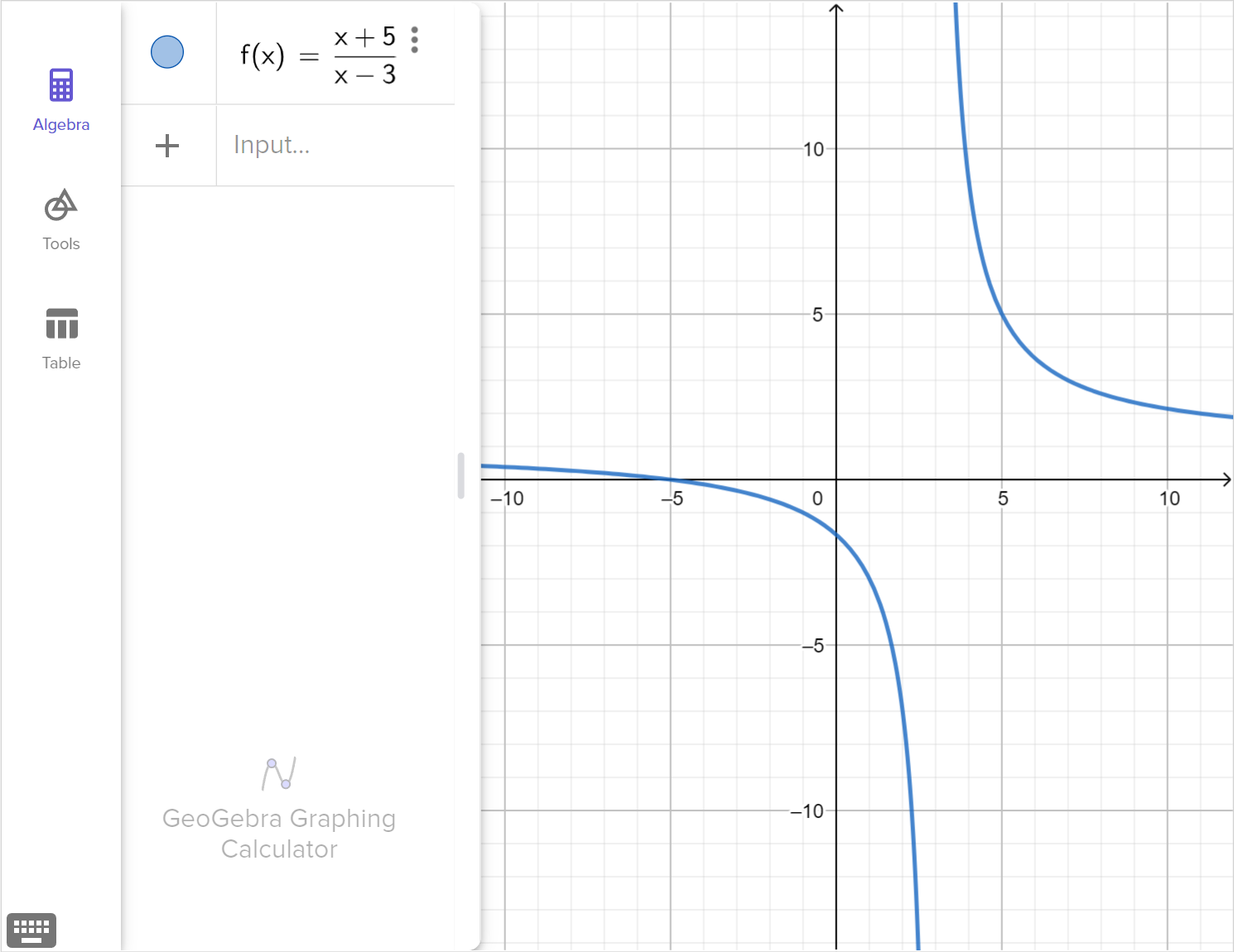
Consider the rational equation:
\frac{x + 5}{x - 3} = 0
Determine whether x = 3 is a viable solution, an extraneous solution, or not a solution at all.
Graph the corresponding function, f\left(x\right)=\dfrac{x + 5}{x - 3}, and explain how any viable solutions, extraneous solutions or restricted domain values are displayed in the graph.
Example 2
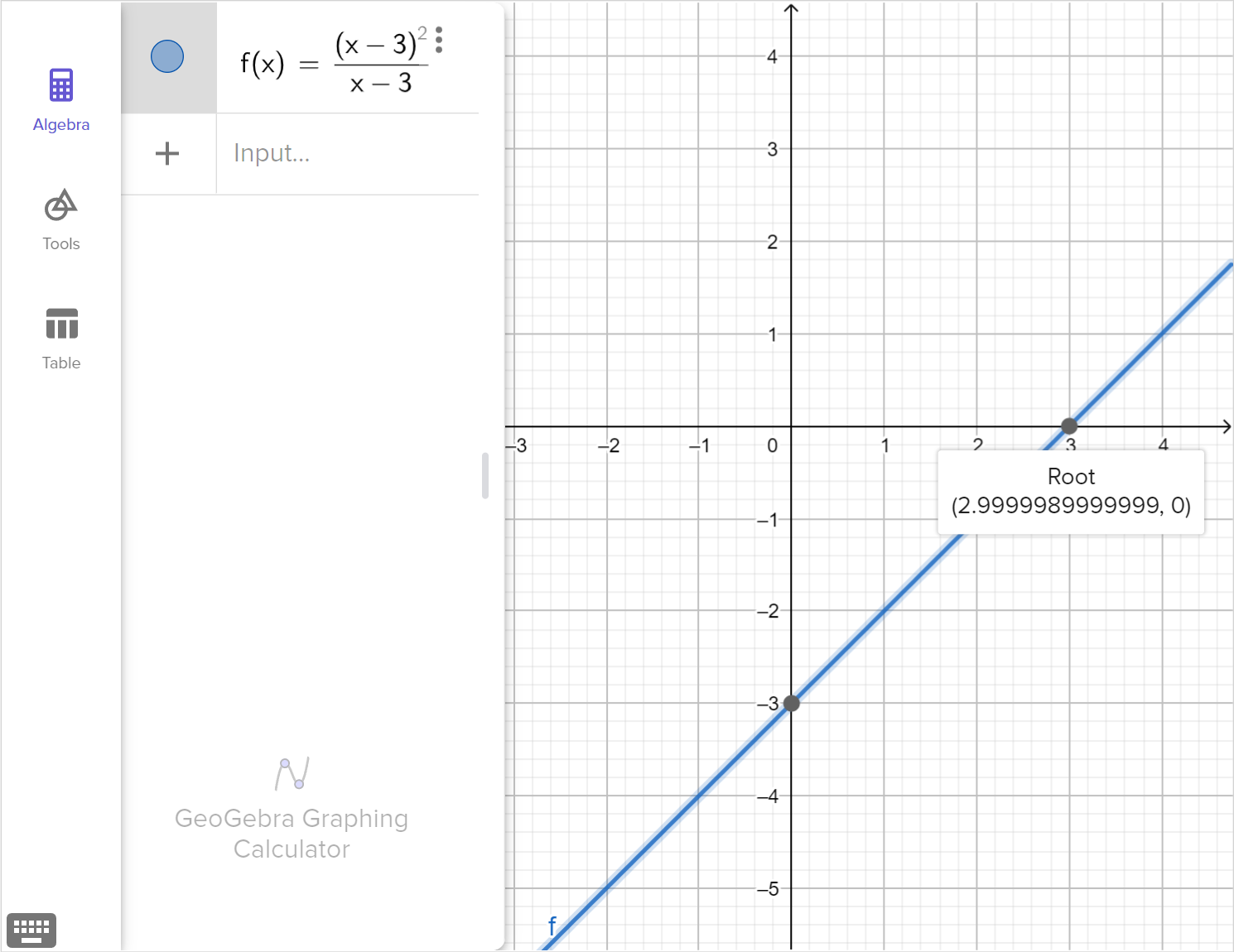
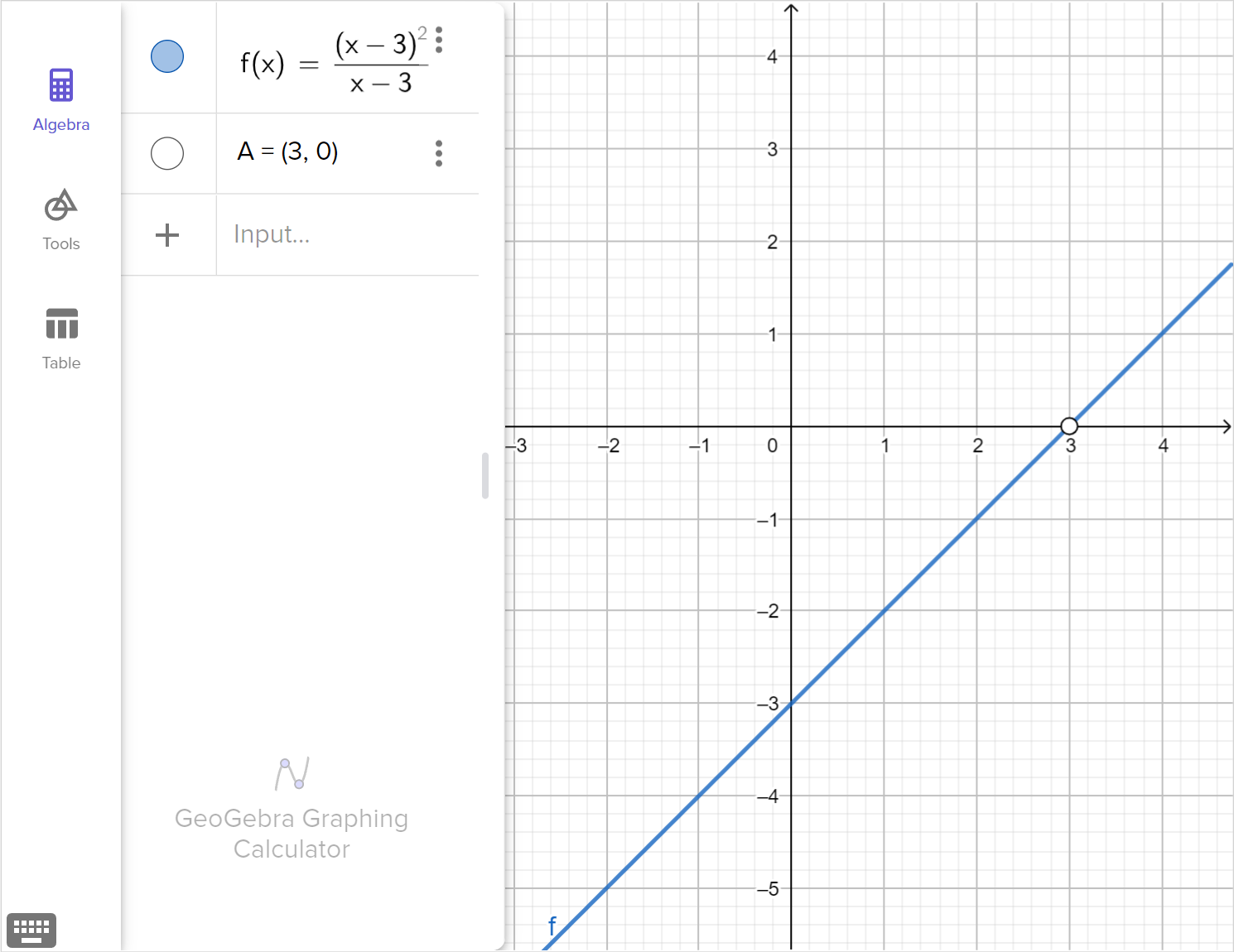
Consider the rational equation:
\frac{\left(x - 3\right)^{2}}{x - 3} = 0
Determine whether x = 3 is a viable solution, an extraneous solution, or not a solution at all.
Graph the corresponding function, f\left(x\right)=\dfrac{\left(x - 3\right)^{2}}{x - 3}, and explain how any viable solutions, extraneous solutions or restricted domain values are displayed in the graph.
Example 3
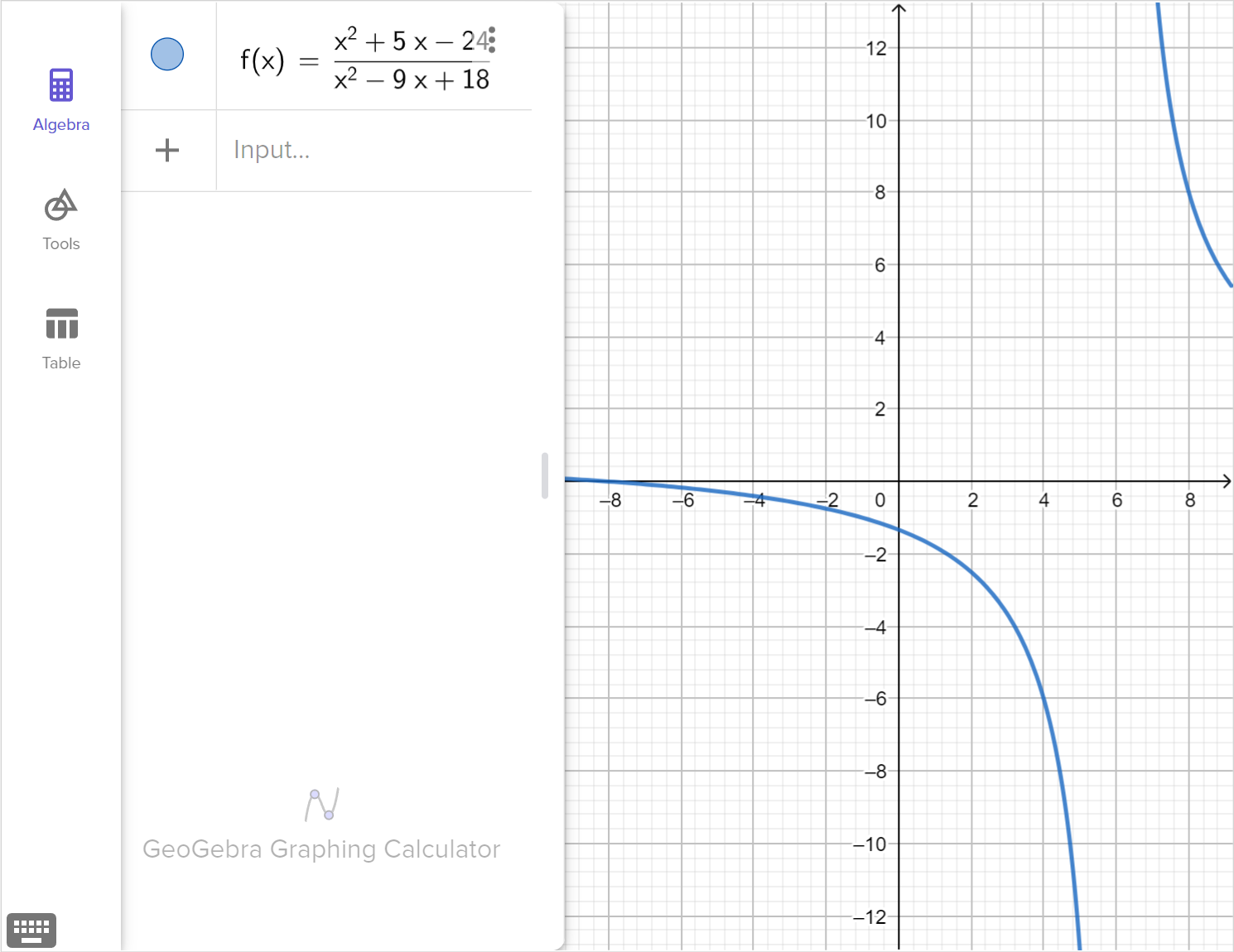
Consider the rational equation:
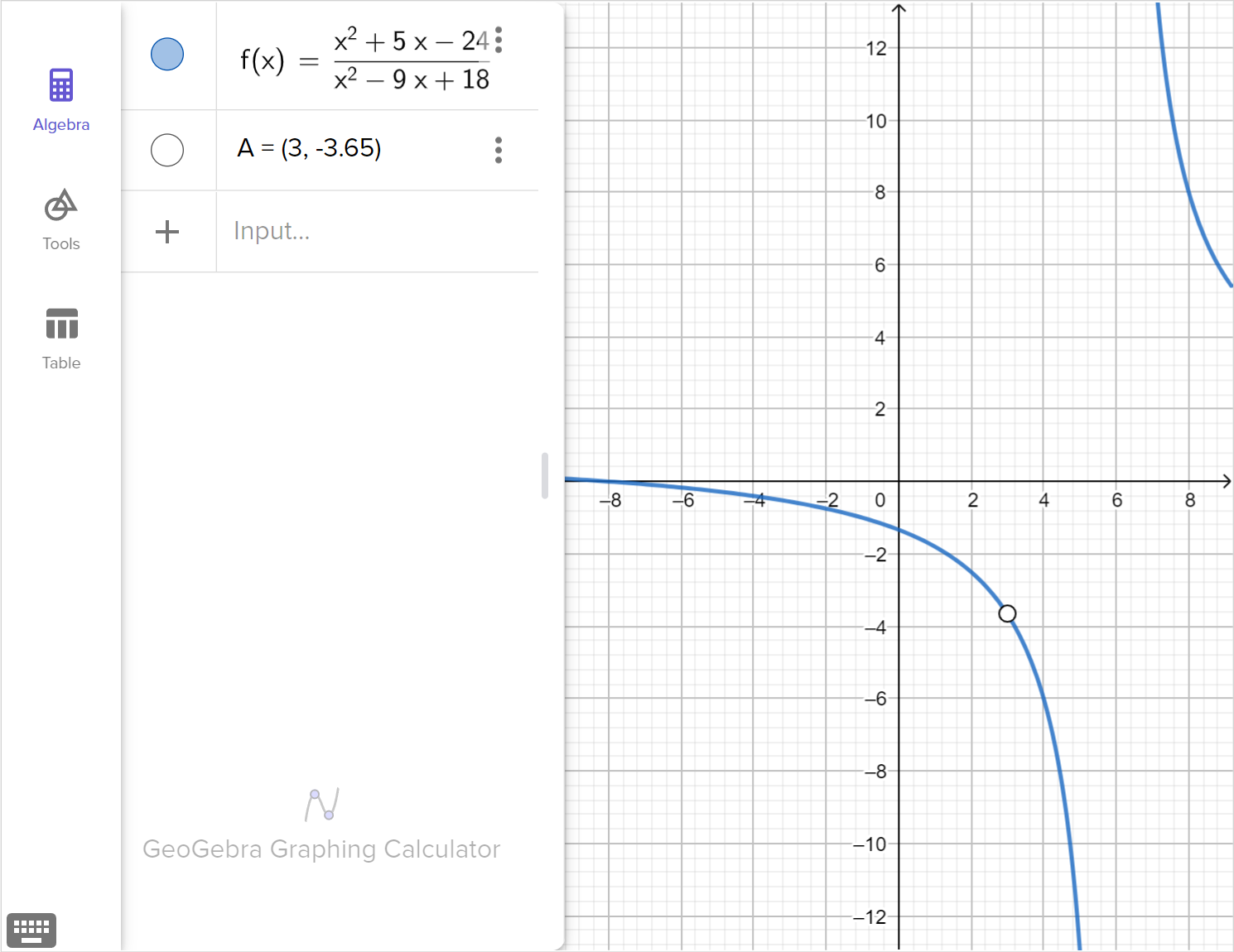
\frac{x^{2} + 5x - 24}{x^{2} - 9x + 18} = 0
Solve the equation.
Graph the corresponding function, f\left(x\right)=\dfrac{x^{2} + 5x - 24}{x^{2} - 9x + 18}, and explain how any viable solutions, extraneous solutions or restricted domain values are displayed in the graph.
Example 4
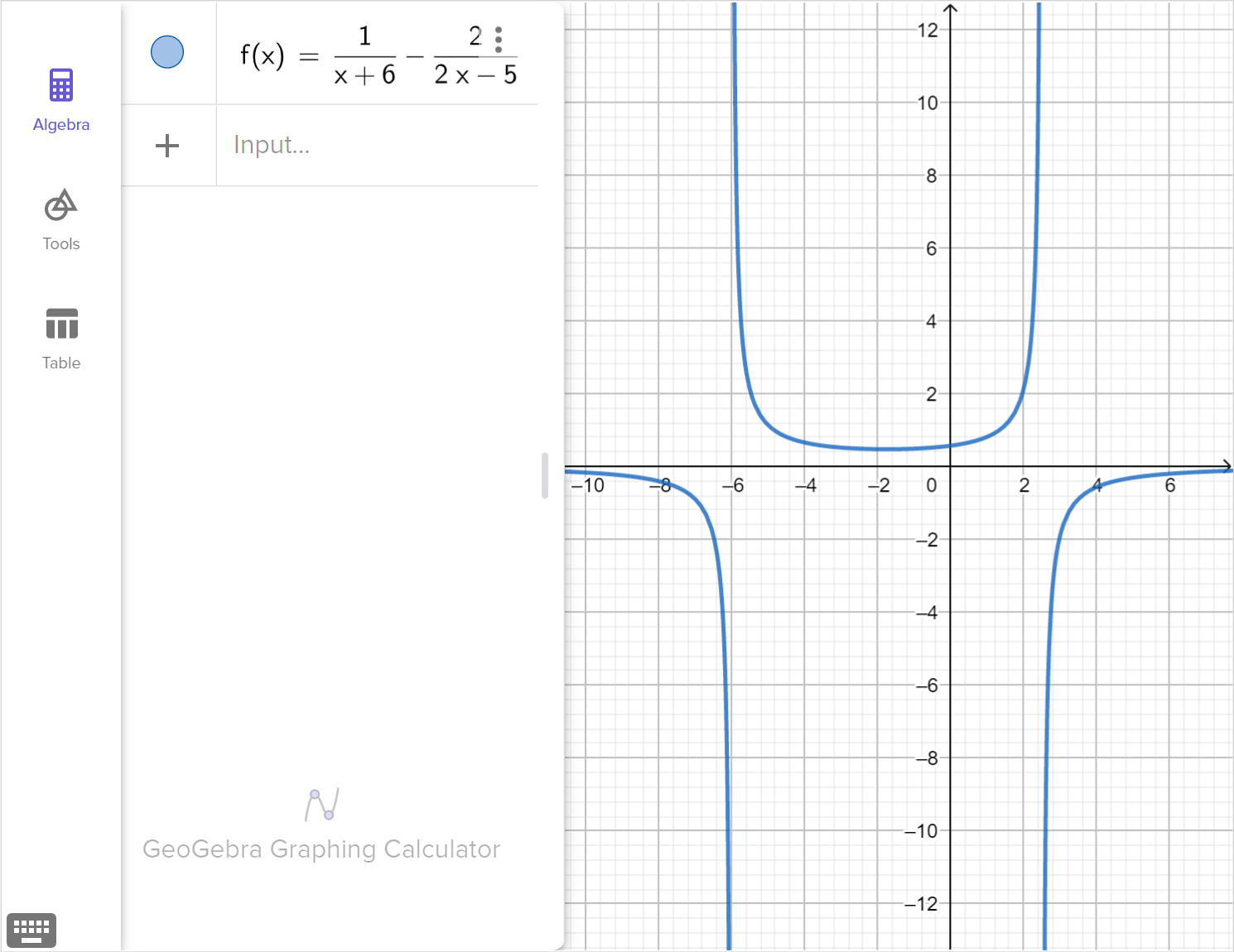
Consider the rational equation:\frac{1}{x + 6} = \frac{2}{2x - 5}
Solve the equation for x.
Graph the corresponding function, f\left(x\right)=\dfrac{1}{x + 6} - \dfrac{2}{2x - 5}, and explain how any viable solutions, extraneous solutions or restricted domain values are displayed in the graph.
Example 5
The Apoleisk Company wishes to calculate the average cost per item of producing car batteries. The fixed monthly cost of production is \$10 \, 000 and each car battery produced costs \$10.
Write the average cost function, A\left(x\right), of producing x car batteries in a month.
State the domain and range of the function.
How many car batteries does the Apoleisk Company need to produce each month so that the average cost of production per car battery is \$60?
We can recognize key features of a rational function by examining zeros and restricted domain values, which can involve factoring the numerator and denominator.
If a solution does not lead to a restriction on the rational function and makes sense within the context of the problem, it is a viable solution.
If there is a value of x that makes the denominator equal to 0, that value must be excluded from the domain of the rational function, which can occur in one of two ways:
- The excluded value also causes the numerator to be equal to 0, and the numerator is of the same or higher multiplicity as the denominator. In this case, the excluded value is an extraneous solution and the graph of the function will have a removable point of discontinuity
- The excluded value does not cause the numerator to be zero, and is not a solution to the equation. The graph will have a vertical asymptote