10.04 Venn diagrams and set notation
A set is a collection of objects that have a common property. So, if you think about all the things in your pencil case, this could be considered a set.

You could list many other sets of objects, such as the clothes you have in your wardrobe, the names of streets you pass by on your way to school, animals that have four legs or people in your family.
To describe a set using mathematical notation, we use large curly brackets and list all the items of the set with a comma between them. Each object in the set is called an element. The set of objects shown in the picture above can be written down as:
$\left\{\text{pencils, pens, sharpener, protractor, scissors, eraser, compass, glue, highlighter, calculator}\right\}${pencils, pens, sharpener, protractor, scissors, eraser, compass, glue, highlighter, calculator}
Of course we can have sets in mathematics as well, and these sets tend to have numbers or algebraic symbols.
The set of odd numbers less than $10$10 would look like this: $\left\{1,3,5,7,9\right\}${1,3,5,7,9}
The set of multiples of $5$5 up to $50$50 inclusive: $\left\{5,10,15,20,25,30,35,40,45,50\right\}${5,10,15,20,25,30,35,40,45,50}
The set of positive factors of $24$24: $\left\{1,2,3,4,6,8,12,24\right\}${1,2,3,4,6,8,12,24}
It is helpful to know that mathematicians call a set with no elements in it an empty set. It is indicated by $\left\{\right\}${} or $\varnothing$∅ .
Intersections and unions
Just like how a road intersection is the place where two roads cross paths, an intersection of sets is where two sets overlap. Elements that appear in the intersection of sets are elements that have the same characteristic as both the individual sets.
Mathematically we write the intersection of sets using the intersection symbol, $\cap$∩. We interpret the intersection of $A$A and $B$B, $A\cap B$A∩B to be what appears in both set $A$A and set $B$B. It helps some students to relate $\cap$∩ to 'AND' or to think of the symbol like a bridge joining both sets.
For example, given the two numerical sets $A=\left\{5,10,15,20,25,30\right\}$A={5,10,15,20,25,30} and $B=\left\{6,12,18,24,30\right\}$B={6,12,18,24,30} then we can find the intersection $A\cap B=\left\{30\right\}$A∩B={30}.
If we consider the intersection the AND of mathematical sets, then the union is the 'OR'. $A\cup B$A∪B is the notation we use, and we would read this as either the union of $A$A and $B$B. The solution is the list of all of the elements that lie in $A$A or $B$B.
For example, given two sets $A=\left\{5,11,16,17,20,25\right\}$A={5,11,16,17,20,25} and $B=\left\{4,12,15,25,30\right\}$B={4,12,15,25,30} we find the union to be $A\cup B=\left\{4,5,11,12,15,16,17,20,25,30\right\}$A∪B={4,5,11,12,15,16,17,20,25,30}.
Visualising multiple sets using Venn diagrams
We are often required to determine whether the information given to us in a practical probability problem involves sets with overlap. As well as using the language and notation of sets as described above, it can be helpful to do this visually.
Imagine you have the following clothes in your wardrobe. This is our Universal set, which simply means that it is the set of everything relevant to this question.

From this we could create two sets, the set $P=\left\{\text{shirts in your wardrobe}\right\}$P={shirts in your wardrobe}

and the set $Q=\left\{\text{blue clothes in your wardrobe}\right\}$Q={blue clothes in your wardrobe}

We now can display this in a Venn diagram, which is made utilising overlapping circles. The idea of a Venn diagram was first introduced by John Venn in the late 1800s and they are still one of the most powerful visualisations for relationships. Imagine you are sorting the objects into two groups.

So we begin sorting our clothes, which is fairly straightforward.

The blue shirt corresponds to both sets, so it is put into the centre overlapping section of the diagram.

Worked example
Example 1
Let's think about the numbers between $2$2 and $20$20.
We are going to create two sets: set $E=\left\{\text{even numbers}\right\}$E={even numbers}, and set $M=\left\{\text{multiplies of 3}\right\}$M={multiplies of 3}.

The next thing to do is write in all the numbers in the appropriate places. As we place a number we consider - is the number even? Is it a multiple of $3$3? Is it both, or is it neither of those options?

Take note of how the numbers that do not fit into either set are placed outside the circles, but still within the bounds of the universal set.
Now that we have a Venn diagram, we can answer a range of questions.
We can list the elements in events $E$E, $M$M and $E\cap M$E∩M:
$E=\left\{2,4,6,8,10,12,14,16,18,20\right\}$E={2,4,6,8,10,12,14,16,18,20}
$M=\left\{3,6,9,12,15,18\right\}$M={3,6,9,12,15,18}
$E\cap M=\left\{6,12,18\right\}$E∩M={6,12,18}
We can also find the complement of a set, which is every element in the universal set not inside a given set:
$M'$M′$=\left\{1,2,4,5,7,8,10,11,13,14,16,17,19\right\}$={1,2,4,5,7,8,10,11,13,14,16,17,19}
$(E\cup M)'$(E∪M)′$=\left\{5,7,11,13,17,19\right\}$={5,7,11,13,17,19}
As you can see, different set notation corresponds to different regions in a Venn diagram. The following applet will let you explore the different regions.
|
|
Practice questions
Question 1
If set $A$A is the set of possible outcomes from rolling a standard die, and set $B$B is the set of possible outcomes from rolling a $\text{D}8$D8 (an eight-sided die):
List the elements of set $A$A.
List the elements of set $B$B.
List the elements of $A\cap B$A∩B.
List the elements of $A\cup B$A∪B.
QUESTION 2
Consider the given Venn diagram.
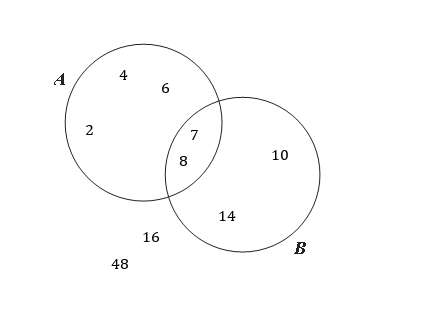
State the elements that belong to $A\cap B$A∩B:
State the elements that belong to $A\cup B$A∪B:
QUESTION 3
The Venn diagram shown shows the number of students in a school playing Rugby League, Rugby Union, both or neither.

How many students play Rugby League only?
How many students play Rugby League?
How many students play Rugby Union?
How many students play Rugby Union only?
How many students do not play Rugby League?
How many students do not play Rugby Union?
QUESTION 4
Consider the diagram below.
List all of the items in:
A Venn diagram is composed of three overlapping circles inside the rectangle labeled $U$U. The top-left circle is labeled $A$A and is shaded blue. The top-right circle is labeled $B$B and is shaded green. The bottom circle is labeled $C$C and is shaded red. Circle $A$A, excluding the overlapping regions, contains the numbers $1$1 and $10$10. Circle $B$B, excluding the overlapping regions, contains the numbers $7$7, $12$12, and $14$14. Circle $C$C, excluding the overlapping regions, contains the number $11$11. The overlapping region between only circles $A$A and $B$B contains the number $3$3 and is shaded light green. The overlapping region between only circles $A$A and $C$C contains the number $9$9 and is shaded light blue. The overlapping region between only circles $B$B and $C$C contains the numbers $8$8 and $6$6, and is shaded pink. The overlapping region of all three circles contains the numbers $4$4 and $5$5, and is shaded in a very light neutral tone. The numbers $2$2 and $13$13 are outside the circles, positioned at the bottom right, but still within the boundary of the rectangle.
$A\cap C$A∩C
$\left(B\cap C\right)'$(B∩C)′
$A\cap B\cap C$A∩B∩C
Mutually exclusive events
If events are mutually exclusive, it means they cannot happen at the same time. The probability of event A and event B happening is therefore zero $P(A\cap B)=0$P(A∩B)=0.
Some examples of experiments that involve mutually exclusive events are:
- tossing a coin - Consider the events 'flipping a head' and 'flipping a tail'. You cannot flip a head and a tail at the same time.
- rolling a die - Consider the events 'Rolling an even number' and 'rolling an odd number'. We can't roll any number which is both even and odd.
- picking a card from a deck of cards - Consider the events 'Drawing a $7$7 card' and 'Drawing a $10$10 card'. They have no outcomes in common. There is no card that is both a $7$7 and a $10$10.
However, some events can happen at the same time and we call this non-mutually exclusive. For example:
- picking a card from a deck of cards - Consider the events 'drawing a Club card' and 'drawing a $7$7'. They have outcomes in common. We could pick a card that is a Club and a $7$7, because we could get the $7$7 of clubs.
- rolling a die - Consider the events 'Rolling an even number' and 'Rolling a prime number'. They have outcomes in common, namely, the number $2$2 .
It's important that we know the difference so that we can accurately answer probability problems that involve the calculation of the union of two events These are the 'either', or the 'or', style of questions we encounter. We have in fact been answering these style of questions already, particularly when we are asked questions about drawing cards from a standard deck.
The mutually exclusive case: $P(A\cup B)=P(A)+P(B)$P(A∪B)=P(A)+P(B)
Consider a card experiment and the events A: 'Drawing a $7$7 card' and B: 'Drawing a $10$10 card'. What is $P(A\text{ or }B)$P(A or B)?
We know that:
| $P(event)$P(event) | $=$= | $\frac{\text{number of favourable outcomes}}{\text{total possible outcomes}}$number of favourable outcomestotal possible outcomes |
| Number of favourable outcomes | $=$= | number of $7$7 cards + number of $10$10 cards |
| $=$= | $4+4$4+4 | |
| $=$= | $8$8 |
Is there any double counting of favourable cards? No, because there are no cards that are both a $7$7 and a $10$10.
| So $\text{P(A or B) }$P(A or B) | $=$= | $\frac{8}{52}$852 |
| $=$= | $\frac{2}{13}$213 | |
| Note: $\text{P(A) }+\text{P(B) }$P(A) +P(B) | $=$= | $\frac{4}{52}+\frac{4}{52}$452+452 |
| $=$= | $\frac{8}{52}$852 | |
| $=$= | $\frac{2}{13}$213 |
$P(A\cup B)=P(A)+P(B)$P(A∪B)=P(A)+P(B)
$P(A\cap B)=0$P(A∩B)=0
The non-mutually exclusive case: $P(A\cup B)=P(A)+P(B)-P(A\cap B)$P(A∪B)=P(A)+P(B)−P(A∩B)
Now, let's consider a card experiment and the events A: 'Drawing a Club card' and B: 'Drawing a $7$7 card'. What is $P(A\text{ or }B)$P(A or B)?
Following our method above, we would get:
| Number of favourable outcomes | $=$= | number of club cards + number of $7$7 cards |
| $=$= | $13+4$13+4 | |
| $=$= | $17$17 |
Do we have any double counting of favourable cards this time? Yes, we do - one card, the $7$7 of clubs. We have counted it twice - once as a club card and once as a $7$7 card. So there are actually only $16$16 favourable outcomes.
It is very easy to spot this when we consider the Venn diagram below.
So:
| $\text{P(A or B) }$P(A or B) | $=$= | $\frac{16}{52}$1652 |
| $=$= | $\frac{4}{13}$413 |
But how can we work this out using the probabilities of the individual events?
Notice:
| $\text{P(A) }+\text{P(B) }$P(A) +P(B) | $=$= | $\frac{13}{52}+\frac{4}{52}$1352+452 |
| $=$= | $\frac{17}{52}$1752 | |
| The overlap of the Venn diagram $P(A\cap B)$P(A∩B) | $=$= | $1/52$1/52 |
| And so, $P(A)+P(B)-P(A\cap B)$P(A)+P(B)−P(A∩B) | $=$= | $\frac{17}{52}-\frac{1}{52}$1752−152 |
| $=$= | $\frac{16}{52}$1652 | |
| $=$= | $\frac{4}{13}$413 |
In actual fact, the relationship above holds for ALL probability events. It's just that when two events are mutually exclusive, $P(A\cap B)=0$P(A∩B)=0 and so we get the shorter formula.
We can work backwards, given probabilities for the union or the intersection of events, to deduce if the events are mutually exclusive. Let's take a look at a question of this type.
Worked examples
Example 2
Consider events A and B such that $P(A\cup B)=0.7$P(A∪B)=0.7, $P(\overline{A})=0.4$P(A)=0.4 and $P(\overline{B})=0.9$P(B)=0.9.
Are events A and B mutually exclusive?
Think: The easiest way to work this out is to firstly represent this information with a Venn diagram.
Do: 
Working with the complements, we can establish $P(A)$P(A) and $P(B)$P(B) as $0.6$0.6 and $0.1$0.1. Since $P(A\cup B)$P(A∪B) is $0.7$0.7, we also know that events outside of A and B have a probability of $0.3$0.3.
Now we consider the value in the middle region, the intersection, of the Venn diagram. Since all other regions add to $1$1, the intersection will be $0$0. Therefore, events A and B are mutually exclusive.
Lastly, we might be asked to create a Venn diagram to answer probability questions given information about the number of objects that fall into certain overlapping categories. In these questions, we are given amounts, rather than probabilities. We can use a modified version of the non-mutually exclusive events formula $n(A\cup B)=n(A)+n(B)-n(A\cap B)$n(A∪B)=n(A)+n(B)−n(A∩B) to first find out the number of items located in the intersection region. We can then fill the remaining regions in our Venn diagram. Finally, we calculate the probabilities as required.
example 3
In a group of $54$54 athletes, $34$34 play soccer and $38$38 play netball. What is the probability that a randomly selected athlete plays
(a) both sports ?
Think: We first need to work out how many athletes play both sports. We know that some must, seeing as $34+38>54$34+38>54.
| $n(A\cup B)$n(A∪B) | $=$= | $n(A)+n(B)-n(A\cap B)$n(A)+n(B)−n(A∩B) |
| $54$54 | $=$= | $34+38-n(A\cap B)$34+38−n(A∩B) |
| $n(A\cap B)$n(A∩B) | $=$= | $18$18 |
Do: We now create a Venn diagram with the intersection region first filled with our value for n(soccer and netball) = $18$18. Since n(soccer) = $34$34, we calculate the number of athletes who only play soccer as $16$16, and using the same logic, the number of athletes who only play netball as $20$20.

Thus, the probability that an athlete plays both sports is $\frac{18}{54}=\frac{1}{3}$1854=13 and
(b) What is the probability they play only soccer?
Do: The probability they only play soccer is $\frac{16}{54}=\frac{8}{27}$1654=827.
Practice questions
Question 5
Two events $A$A and $B$B are mutually exclusive.
If P(A) = $0.37$0.37 and P(A or B) = $0.73$0.73, what is P(B)?
Question 6
Consider the following probability Venn diagram:

A Venn diagram consist of two overlapping circles. The circle on the left is labeled $A$A. The circle on the right is labeled $B$B. The overlapping region contains the bold variable $x$x. Inside circle $A$A but excluding the overlapping region, a number $0.7$0.7 is written. Inside circle $B$B but excluding the overlapping region, a number $0.1$0.1 is written. Outside both circles, positioned near the bottom right of circle $B$B, a number $0.2$0.2 is written.
Calculate the value of $x$x in the diagram. Enter your answer as an equation in $x$x.
Are events $A$A and $B$B mutually exclusive?
Yes
ANo
B
Question 7
Use the formula $P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$P(A∪B)=P(A)+P(B)−P(A∩B) to solve the following question.
If $P\left(A\right)=\frac{1}{3}$P(A)=13, $P\left(B\right)=\frac{1}{5}$P(B)=15 and $P\left(A\cup B\right)=\frac{2}{15}$P(A∪B)=215, find $P\left(A\cap B\right)$P(A∩B).

