Lateral area of prisms

Lesson

Practice

Lesson

To create a prism we start with a base or end face. This could be a familiar shape like a right-triangle, a square, a trapezoid or a pentagon. Or we could use some kind of irregular polygon with many different side lengths.

Our prism will have two identical bases. The two bases are joined together by the lateral faces.

A quadrilateral prism, with two bases and four lateral faces.

The lateral area of a prism is the total surface area of all the lateral faces. For any prism, the lateral faces will always be rectangles, so we can find the area of each lateral face using the formula for the area of a rectangle.

The lateral area of a prism

Each lateral face of a prism is a rectangle whose area $A$A is given by $A=bh$A=bh, where

$b$b is the base
$h$h is the height

If we sum the area of each lateral face of a prism, the total is the lateral area of the prism.

Worked example

Find the lateral area of the following triangular prism.

Think: The base is a triangle with three edges, so there are three lateral faces, one for each edge of the triangle. All three lateral faces will have the same height of $12$12 m, equal to the length of the prism.

Explore the applet below to see how the prism is made up of two triangular bases and three rectangular lateral faces.

Created with Geogebra

Do: Since each lateral face is a rectangle, we can use the formula for the area of a rectangle $A=bh$A=bh. We will label the lateral faces $A_1$A1, $A_2$A2, and $A_3$A3.

$A_1$`A`1:	$A$`A`	$=$=	$bh$`bh`
		$=$=	$3\times12$3×12
		$=$=	$36$36 m²

$A_2$`A`2:	$A$`A`	$=$=	$bh$`bh`
		$=$=	$4\times12$4×12
		$=$=	$48$48 m²

$A_3$`A`3:	$A$`A`	$=$=	$bh$`bh`
		$=$=	$5\times12$5×12
		$=$=	$60$60 m²

Lateral area:	$A$`A`	$=$=	$A_1+A_2+A_3$`A`1+`A`2+`A`3
		$=$=	$36+48+60$36+48+60
		$=$=	$144$144 m²

So the triangular prism has a lateral area of $144$144 m².

Reflect: Notice that the area of each lateral face is a multiple of $12$12, the length of the prism. We can write the lateral area of the prism as $12\left(3+4+5\right)$12(3+4+5), where the sum $\left(3+4+5\right)$(3+4+5) represents the perimeter of the base.

Practice questions

Question 1

Consider the following closed rectangular prism with length of $12$12 m, width of $8$8 m and height of $24$24 m.

A closed rectangular prism is illustrated with dimensions labeled on it. The base is a rectangle with a length of $12$ m and a width of $8$ m. The prism's height, which extends upward from the base, is measured as $24$ m. The figure's edges are depicted by solid lines, except for the edges on the back of the prism, which are represented by dotted lines.

How many lateral faces does this prism have if the base is the side that is $8$8 m by $12$12 m?
$1$1
A
$4$4
B
$2$2
C
$6$6
D
Find the area of the lateral face, which is the rectangle with base $12$12 m and height $24$24 m.
Find the area of the lateral face, which is the rectangle with base $8$8 m and height $24$24 m.
Find the lateral area of the prism.

Question 2

Consider the following prism.

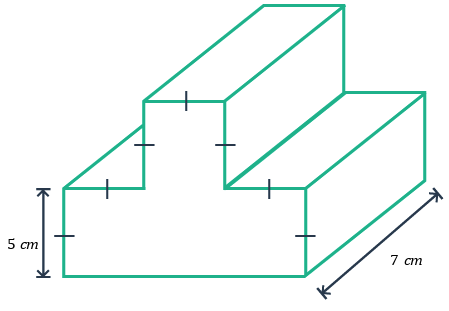
How many lateral faces does this prism have?

$\editable{}$
How many of the lateral faces are $5$5 cm by $7$7 cm?

$\editable{}$
Find the lateral area of the prism.

Question 3

Consider the following rectangular prism. Let the face with sides $w$w, $x$x, $y$y, and $z$z be the base.

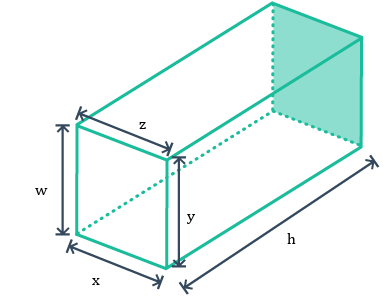
Write an expression for the sum of the area of the four lateral faces.
Factor the expression from part (a).
What does the expression $w+x+y+z$w+x+y+z represent for this prism?
Perimeter of the base.
A
Area of the base.
B
The surface area.
C

Outcomes

6.M2.09

Determine, through investigation using a variety of tools (e.g., nets, concrete materials, dynamic geometry software, Polydrons) and strategies, the surface area of rectangular and triangular prisms