7.06 Polygons in the coordinate plane
Polygons in the coordinate plane
Remember that the coordinate plane can be used to describe the location of points in a 2D space.
Using the points A(-1,\,1),\,B(3,\,1),\,C(3,\,3),\, and D(-1,\,3) we can draw quadrilateral ABCD. We can calculate the side lengths of the ABCD using the ordered pairs.
We can use these side lengths to calculate perimeter and area from polygons on the coordinate plane.
Recall, the perimeter of a rectangle can be found by adding up all of the side lengths, or using the formula P=2l+2w and here l=4 units and w=2 units. So:
P=2(4)+2(2)=8+4=12 \text{ units}
The area of a rectangle can be found using the formula A=bh where the base and height are the same as the length and width we used to find the perimeter. So:
A=4 \cdot 2=8 \text{ units}^2
Examples
Example 1
What are the coordinates of the vertices of this quadrilateral?
Example 2
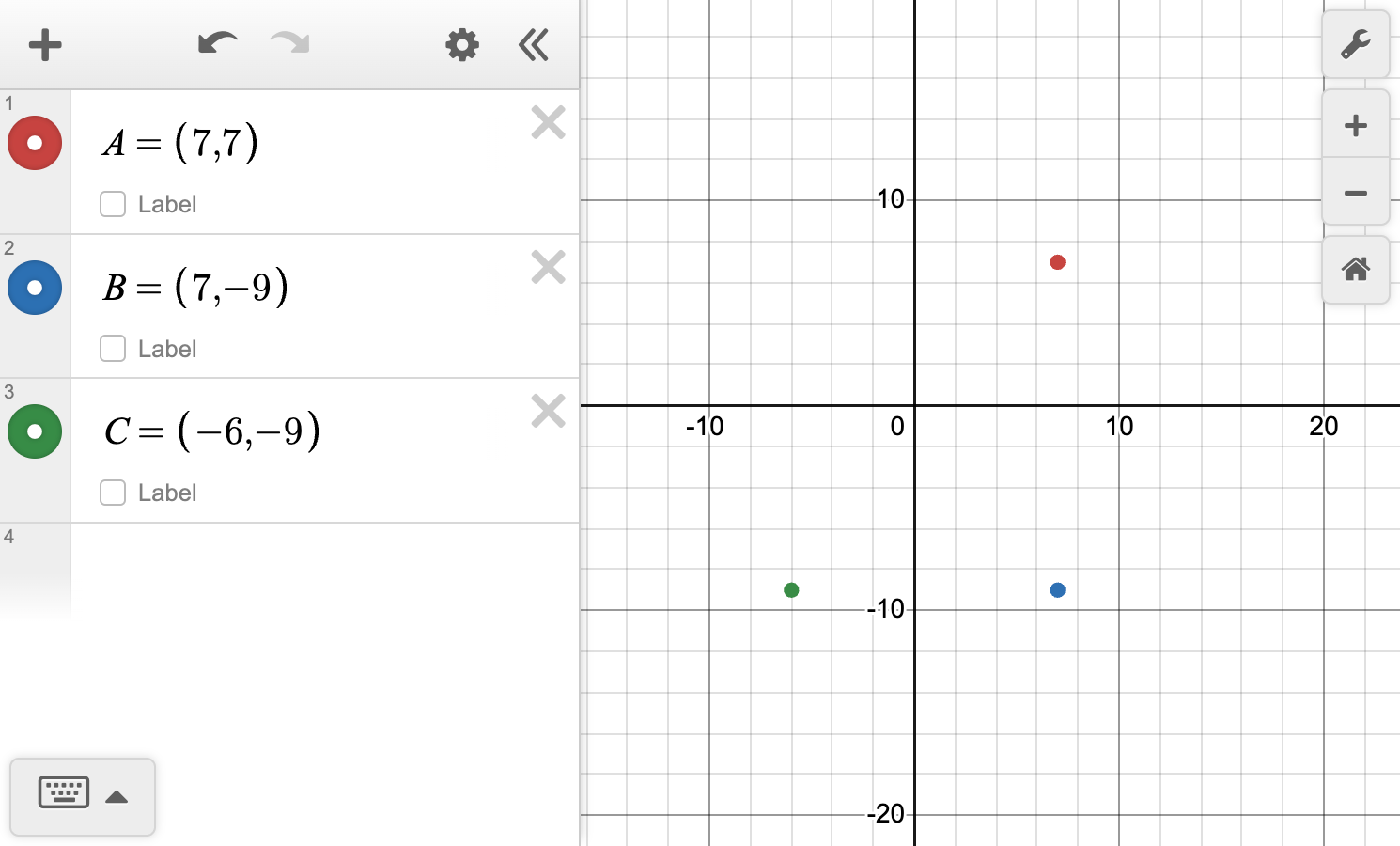
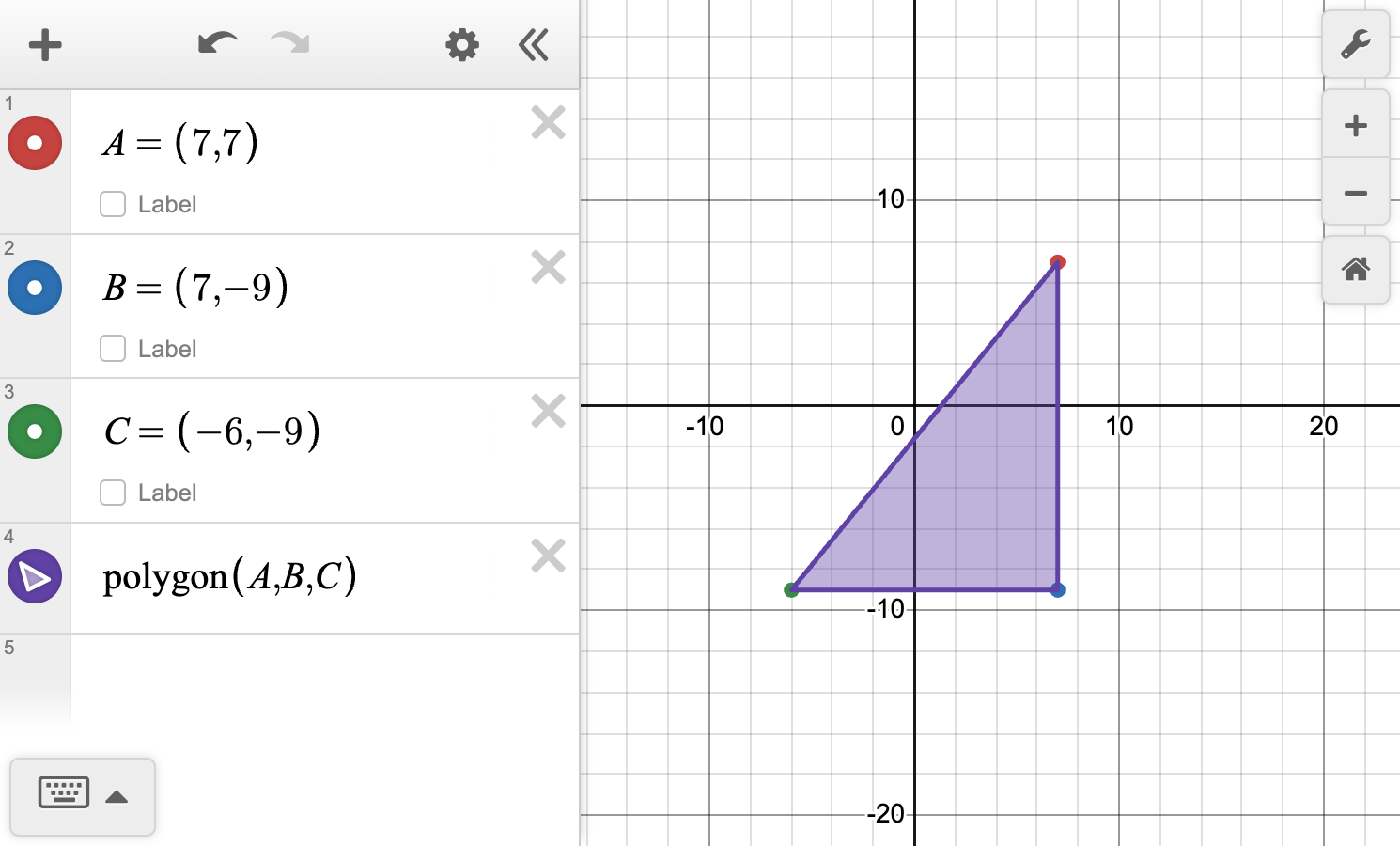
Consider the points A\left( 7,\,7\right),\,B\left( 7,\,-9\right) and C\left( -6,\,-9\right).
Plot the points on the coordinate plane.
What is the length of AB?
Find the length of BC
Find the area of \triangle ABC
Example 3
Consider the square LMNO.
Find the perimeter of LMNO.
Find the area of LMNO.
To find the distance between two points with the same x-coordinates, subtract the y-coordinates and then find the absolute value of the difference.
The same is true for points with the same y-coordinates. Subtract the x-coordinates and then find the absolute value of the difference.
We can also find the distance between points that share an x- or y-coordinate, by counting the number of spaces between them on the coordinate plane.