9.05 Analyze bivariate data
Analyze bivariate data
The process of analyzing bivariate data involves a two-step process. First, we plot the data on a scatterplot. This allows us to visually inspect the relationship between the two variables. Then, we use mathematical models to describe this relationship. Two common models that we have used are the linear regression model and the quadratic regression model.
Exploration
Check a box to show a linear or quadratic model. Drag the points with the blue circles to fit the model to the data on the graph.
Which function fits the data better? How do you know?
To determine the curve of best fit for a set of bivariate data, we can use technology such as graphing calculators or software. These tools allow us to perform both linear and quadratic regression on the same set of data and compare the results.
To decide which curve best models the data, we can visually assess whether the curves follow the trend in the data and how close the points are to each curve. We can also use the context to determine if a model is a good fit.
In the models shown, we can see the data points more closely follow the quadratic curve. Especially upon inspection of x-values closer to 0, the quadratic model more closely aligns with the data in the scatterplot. A better model will have data that is more tightly clustered along the curve.
Examples
Example 1
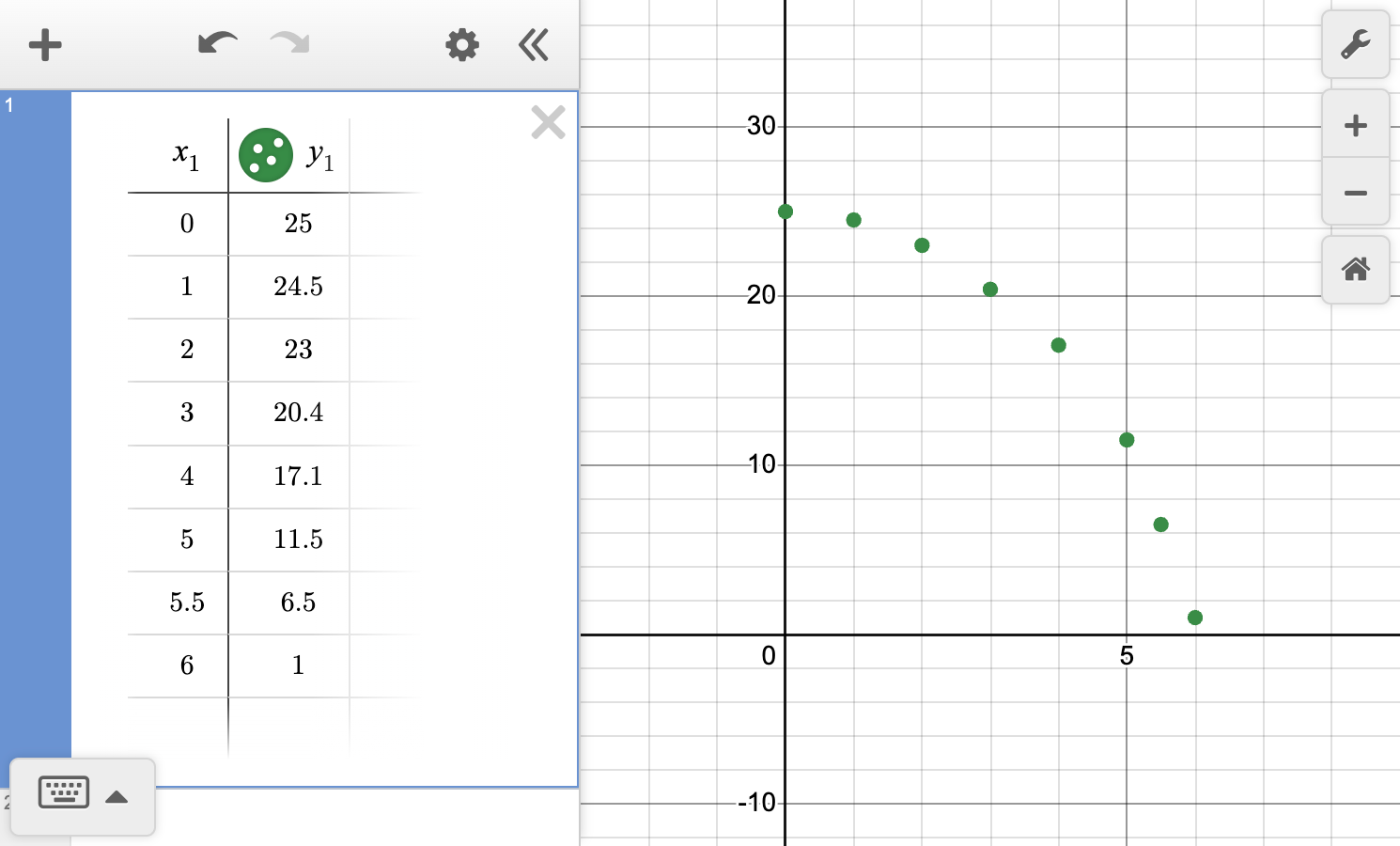
A ball is dropped off of a building that is 25 feet high. The table below shows its distance from the ground over time.
| Time since being thrown (seconds) | 0 | 1 | 2 | 3 | 4 | 5 | 5.5 | 6 |
|---|---|---|---|---|---|---|---|---|
| Distance from ground (feet) | 25 | 24.5 | 23 | 20.4 | 17.1 | 11.5 | 6.5 | 1 |
Describe the relationship between the time since the ball was dropped and its distance from the ground. Is it quadratic or linear?
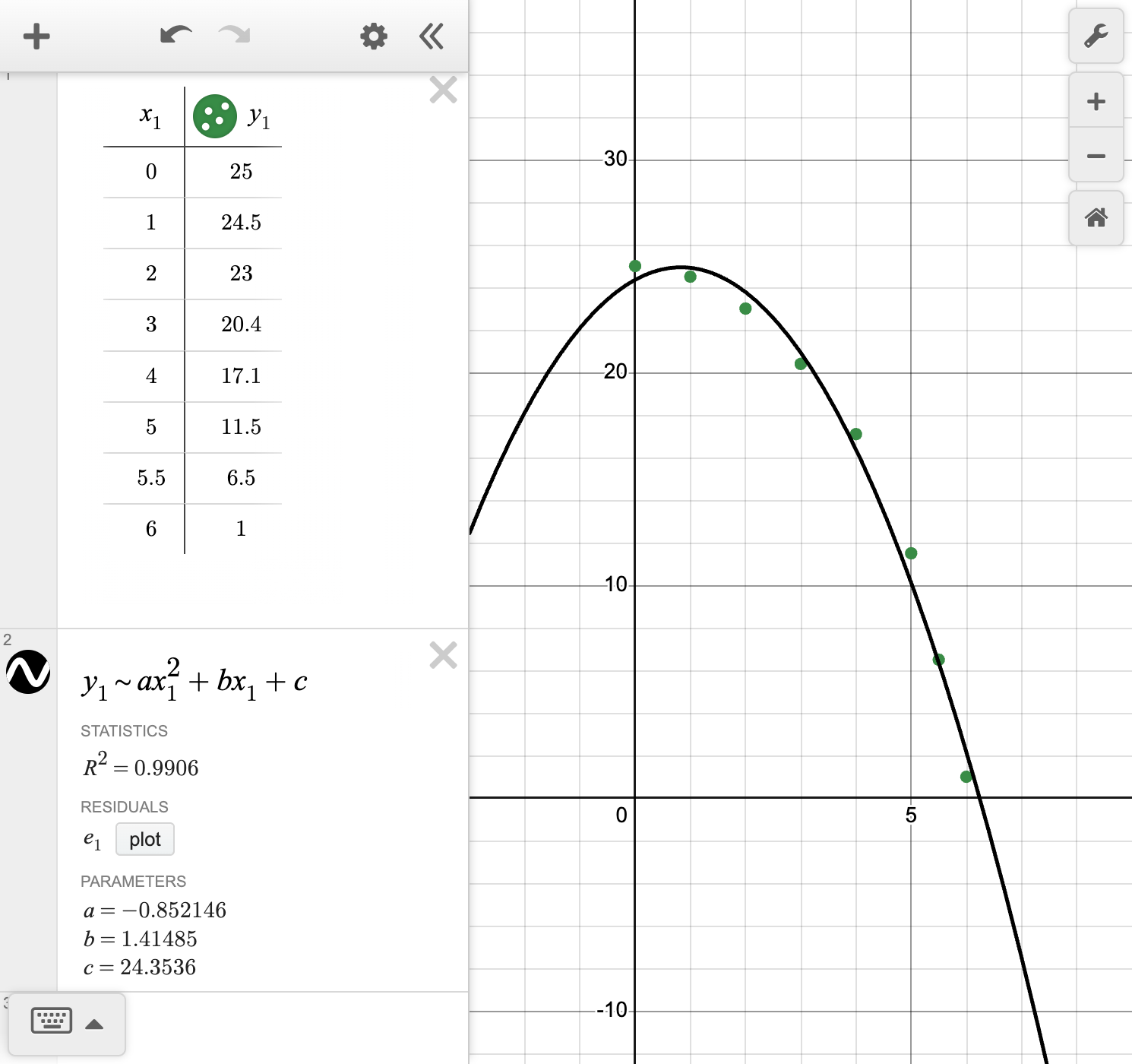
Use technology to create a model and graph the model alongside a scatterplot of the data.
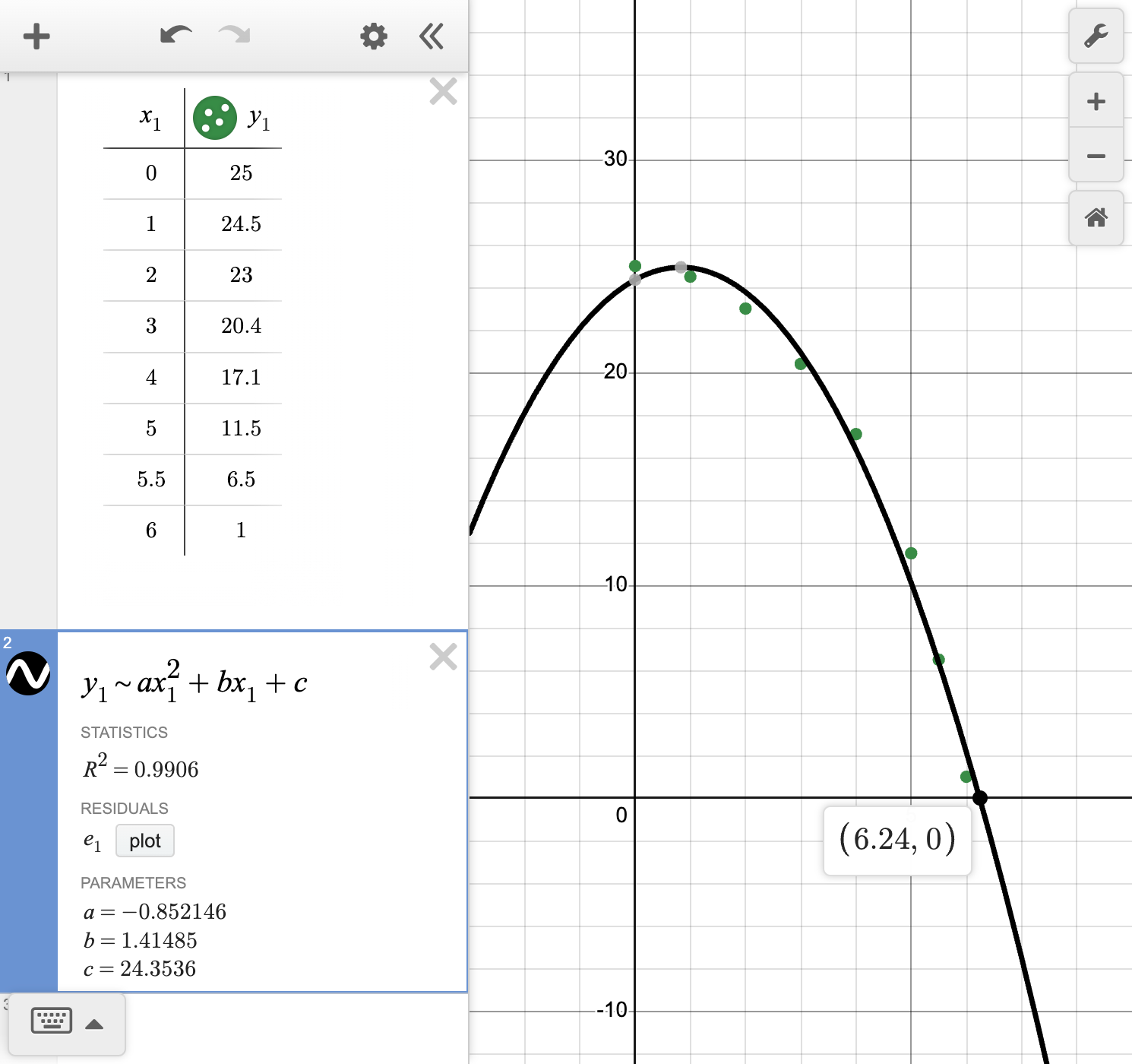
Based off your model, when would you predict the ball would hit the ground?
Example 2
Ronaldo is looking to rent a two-bedroom apartment. He wants something that is spacious, but affordable. He decides to use the data cycle to explore rental options in his area.
Identify the two variables that Ronaldo should collect data for in his investigation of potential apartments and then formulate a statistical question to investigate them.
Collect data that could be used to answer the statistical question you formulated.
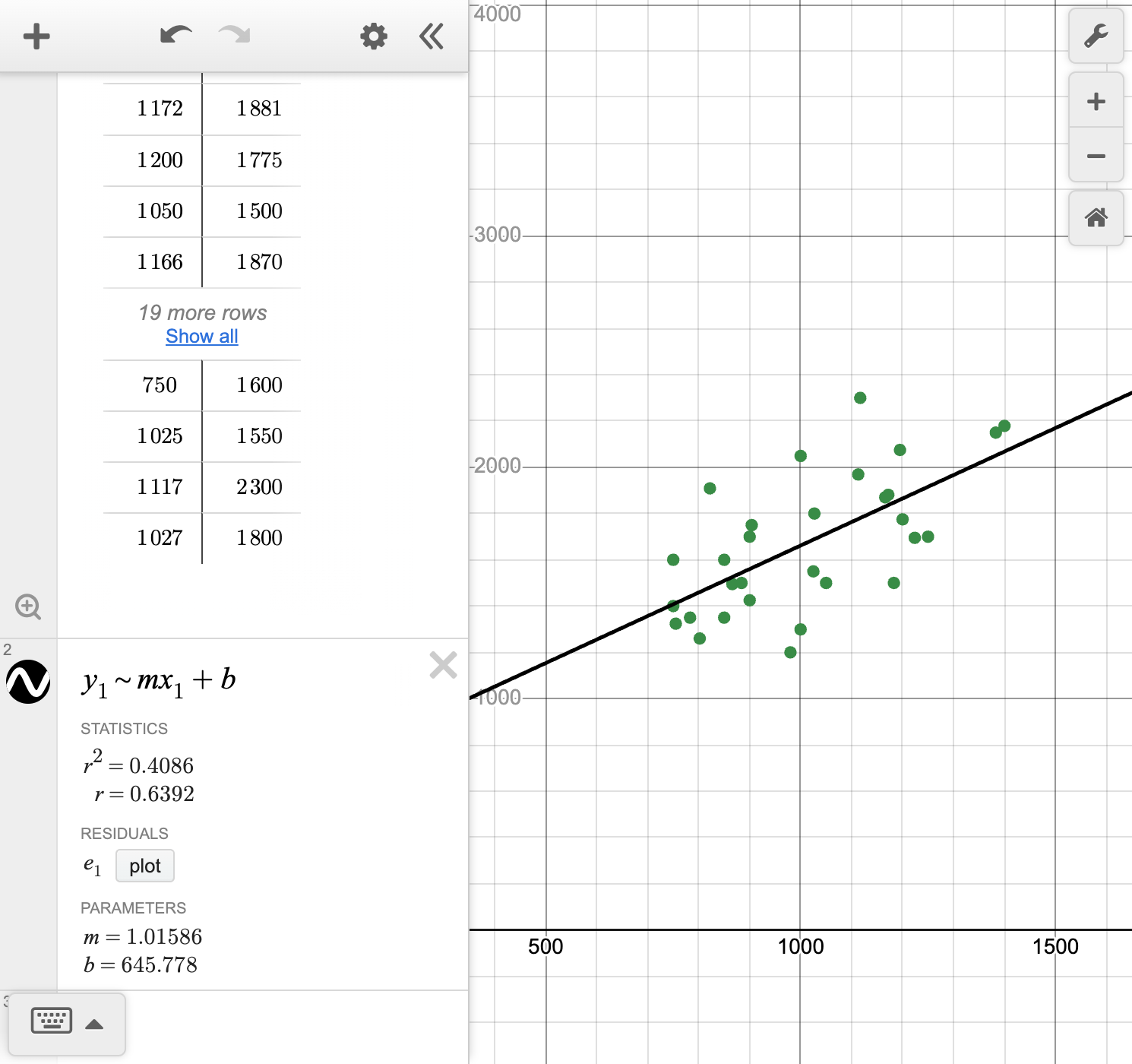
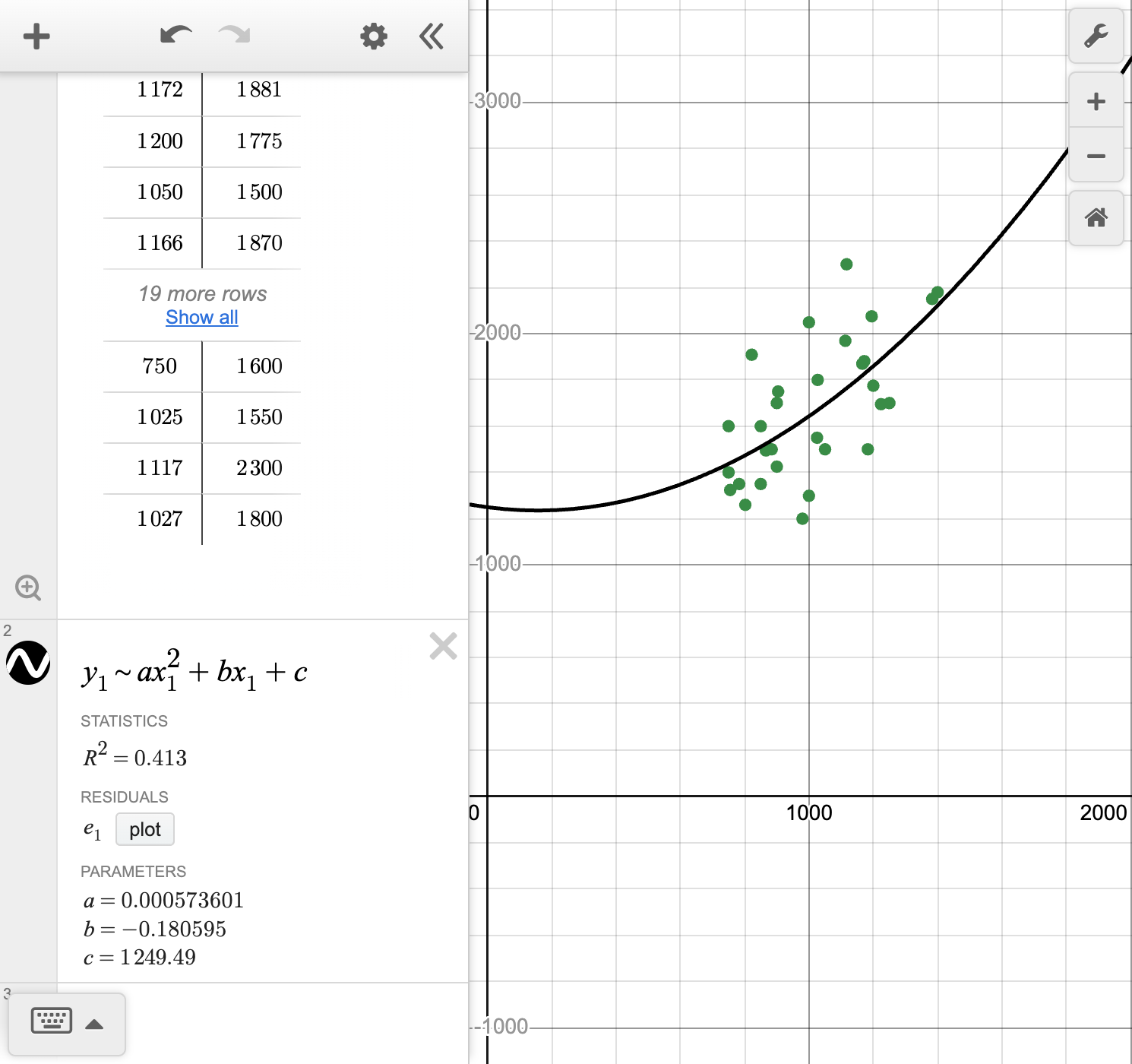
Determine whether a linear or quadratic function would represent the relationship best. Calculate the equation of the curve of best fit.
Ideally, Ronaldo would like an apartment that is 1100\text{ ft}^2. Predict the monthly rental price of an apartment of this size.
Ronaldo's budget is \$1650. Predict the size of the apartment he can afford.
Draw a conclusion by answering the statistical question from part (b) and summarize the results of the investigation.
We can use technology to analyze bivariate data by creating and comparing regression models. To choose the model with the best fit, we analyze the visual fit on the scatterplot and the context of the problem. If the points are clustered more closely, the model is the better fit.